Vallen Systeme VisualAE – Математический и встроенный программный процессоры

Настоящий обзор посвящен двум процессорам Visual AE, которые позволяют кратно усилить возможности анализа данных АЭ. Это математический процессор (или процессор пользователя) и ECP процессор (встроенный программный процессор). Процессоры похожи по назначению и принципам действия, поэтому включили их в один обзор.

Математический (пользовательский) процессор

Использование МП дает возможность, выполняя определенные математические действия над существующими данными, определять новые параметры, по которым можно осуществлять фильтрацию, которые можно использовать на диаграммах, помещенных после математического процессора, и над которыми также можно выполнять операции. Так, например, с помощью математического процессора может быть оценено выполнение эффекта Кайзера, оценка энергетической интенсивности источников АЭ. Процессор включает статистические функции, выражения, функции оценки скорости изменения параметра, функцию коррекции амплитуды.

Общая концепция процессора:

В окне процессора задаются один или более новых параметров. Вновь созданный параметр может использоваться в другом параметре, в этом же МП, но тогда он должен располагаться перед (выше) того параметра, в котором используется. Данная опция значительно расширяет возможности процессора.

Сами новые параметры определяются в соответствующих диалоговых окнах, конкретное наполнение которых зависит от типа используемых функций.

Вновь создаваемый параметр относится к одному из типов данных, определяемых в нижней части диалога:

• Автоматический выбор
• Только записи опроса состояния системы
• Только записи опроса параметрических входов
• Импульсы / Зарегистрированные события / Лоцированные события

Как правило, достаточно использовать автоматический выбор.

Параметры могут создаваться на базе традиционных АЭ параметров (или новых параметров) с использованием следующих групп функций:

• Статистические (Statistic)
• Операторы (Operators)
• Линейные функции (Linear Scale)
• Функция коррекции амплитуды (Amplitude Correction)
• Функции скоростей (Rates)

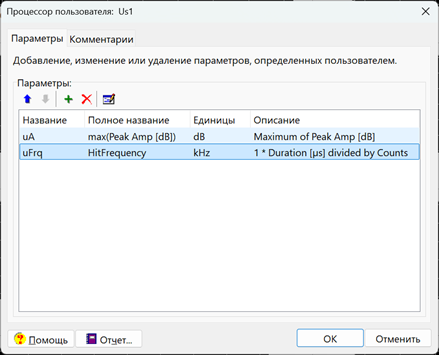
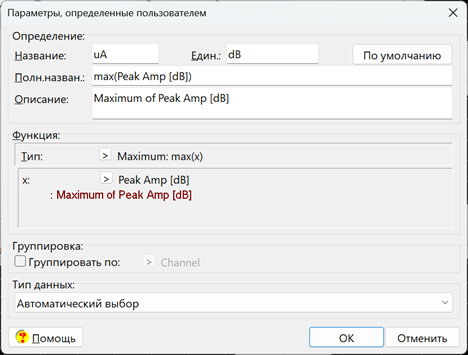
Рис. 1. Окно процессора пользователя. Окно определяемого параметра

В результате работы МП появляется новый параметр и этот параметр принадлежит тому типу записей, для которой создавался (как правило, записи импульса). При этом значение параметра может основываться на значениях параметров этой же записи (например, Частота= Кол-во выбросов/Длительность) или на значениях параметров нескольких записей (например, максимальная амплитуда). Во последнем случае возможна группировка параметра по каналам, т.е. значение параметра может вычисляться для каждого канала индивидуально (группированы по каналам могут Статистические функции и Функции скоростей). В первом же случае группировка по каналам не имеет смысла, т.к. функция работает в пределах одной записи.

Нужно понимать, что формирование новых параметров происходит последовательно от первой записи (например, импульса) к последней и каждое вычисление нового параметра для текущей записи оперирует данными от первой до этой записи. Т.е. конечное значение нового параметра будет иметь место у последней записи (см., например, параметр Max()).

МП может быть использован для получения значения локационной амплитуды лоцированных событий, причем вычисление этой амплитуды производится согласно положениям стандарта EN 14584, «прозрачно» и контролируемо, с учетом затухания в ближней и дальней зонах, производные параметры могут использоваться в любых процессорах VisualAE так же, как и обычные параметры АЭ, использоваться как критериальные (максимальные, суммарные значения, скорости накопления параметров), использоваться как дополнительные параметры АЭ импульсов – такие, как, например, соотношения Времени Нарастания и Длительности, Количества Выбросов и Длительности для оценки и фильтрации.

Статистические функции

Группа статистических функций включает Минимальное, максимальное, суммарное, среднее значение параметра, дисперсию, стандартное отклонение, изменение среднего значения.

• Min(x1…xN):                                  Минимальное значение параметра x₁…x_N
• Max(x1…xN):                                 Максимальное значение параметра x₁…x_N
• Sum(x1…xN):                                 Суммарное значение параметра x₁…x_N
• Mean(x1…xN):                               Среднее значение параметра Sum(x₁…x_N)/N
• Variance: Var(x1…xN)                   Дисперсия параметра [1/(N-1)]*Sum[(x_i-x_mean)²]
• Std. Dev.: Stddev(x1…xN)            Стандартное отклонение параметра Var(x₁…x_N)^1/2
• Average Change                           Среднее изменение [1/N * Sum(dx^-2)]^1/2, где dx: x_N-x_N-1
• Deviation: x(N)-x(N-1)                  Отклонение — текущее значение минус предыдущее x_N-x_N-1

Для справки:

Дисперсия (variance) – мера разброса случайной величины от ее математического ожидания, среднее значение квадратов отклонений каждой точки данных от среднего. Она измеряет, насколько данные разбросаны относительно среднего.

Стандартное отклонение (среднеквадратичное отклонение, standard deviation) – показатель рассеивания значений случайной величины от ее математического ожидания. Квадратный корень из дисперсии. Показывает, какова величина разброса данных в тех же единицах, что и сами данные. Т.о. дисперсия – это мера разброса, выраженная в квадрате единиц измерения, а среднеквадратичное отклонение – в тех же единицах, что и данные.

Среднее изменение (Average Change) можно интерпретировать как меру изменчивости данных, где меньшие изменения вносят больший вклад в итоговое значение. Это может быть полезно в случаях, когда нужно акцентировать внимание на стабильности данных.

Применение:

Диаграмма, иллюстрирующая эффект Кайзера/Фелисити (см. Рис. 2), приводится во многих источниках, однако практическое ее построение встречает ряд трудностей — необходима либо диаграмма заведомо определенного типа, либо отдельный тип данных (например, порядковый номер импульса), либо раздельное построение диаграммы для разных этапов нагружения.

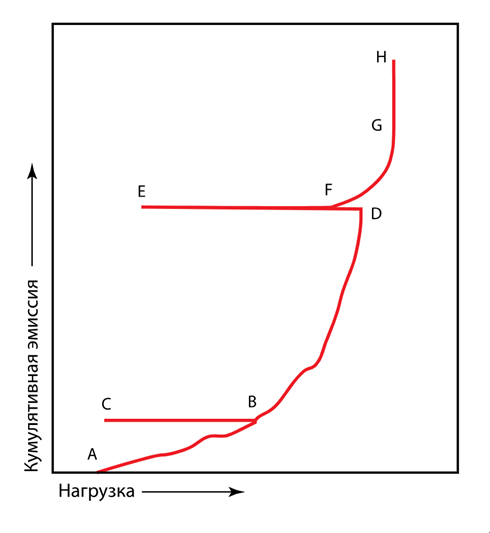
Рис. 2. Эффект Кайзера/Фелисити

В VisualAE диаграмма, иллюстрирующая эффекта Кайзера/Фелисити (см. Рис. 3) с помощью МП легко строится не только для любого зарегистрированного или сформированного АЭ параметра (количества импульсов, выбросов, длительности и т.п.) и параметра нагружения (от датчика давления или искусственно введенного), но и для каждого канала (с помощью группировки). При нахождении в соответствующей позиции в структуре данных диаграмма может относиться, например, только к лоцированным событиям.

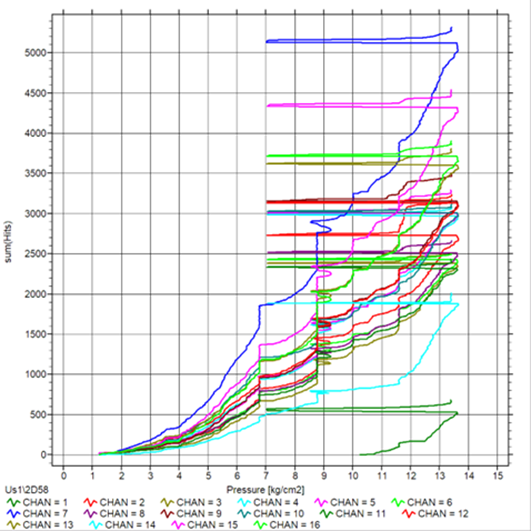
Рис. 3. Иллюстрация выполнения эффекта Кайзера

Для построения диаграммы необходимо в математическом процессоре задать новый параметр – сумму импульсов, сумму выбросов или какой-то иной параметр (Sum(A) или Sum(N)).  Для разделения информации по каналам необходимо включить группировку. Далее строится диаграмма (корреляция, стиль серии – линия). Результат представлен на Рис. 3.

На Рис. 4 показаны результаты формирования нового параметра – частоты импульса, в килогерцах (см. ниже), дисперсия и стандартное отклонение частоты импульсов по ходу испытания. Для формирования всех параметров использовался один МП.

Выражения и линейные функции

Группа выражений включает отношение, произведение, сумму, степень, логарифмические, линейные функции, касающиеся одного или двух параметров.

• Ratio: A*x/y                      Операция деления двух параметров
• Product: A *x*y                Операция умножения двух параметров
• Power: A *x^K                  Операция возведения в степень
• Add: (A * x) + (B * y)       Операция суммирования двух параметров
• Log: A * log(x), Base B    Операция логарифмирования по основанию B
• Logn: A * In(x)                  Операция логарифмирования по основанию e (натуральный логарифм)
• (A * x) + B                           Линейная функция A * (x + B)                           Линейная функция

Применение:

Функции группы «Выражения» могут применяться для создания новых параметров (например, Частота, кГц = 1000*Количество выбросов/Длительность, мкс, см. Рис. 4).

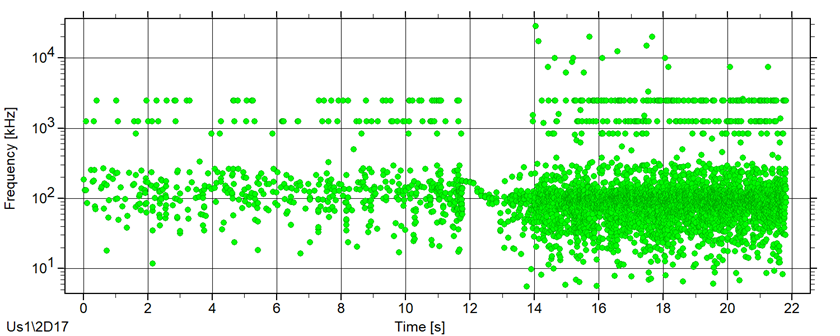
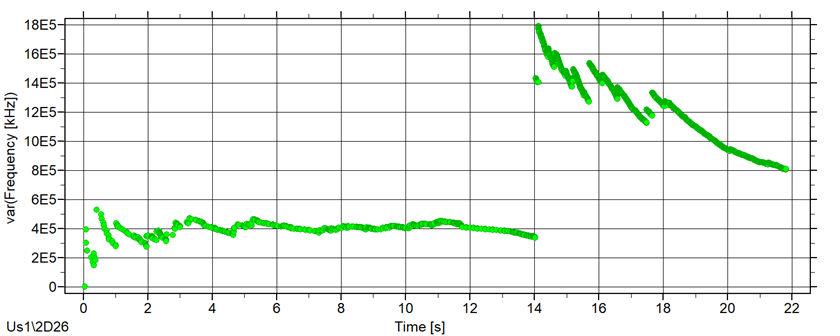
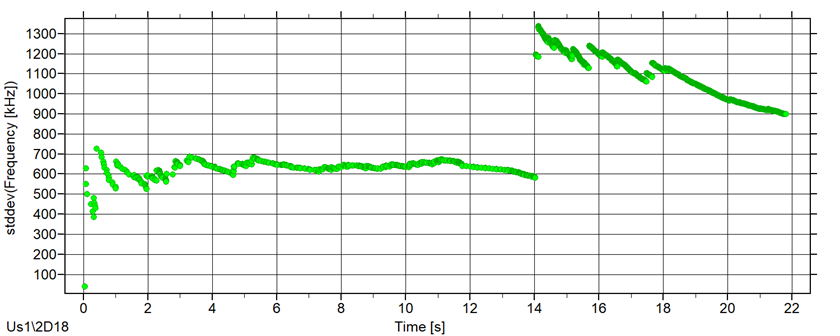
Рис. 4. Частота импульсов АЭ, кГц, дисперсия и стандартное отклонение частоты

Функция коррекции амплитуды

Функция коррекции амплитуды выполняет коррекцию амплитуды (определение первичной амплитуды сигнала АЭ по данным затухания) в соответствии с положениями стандарта EN14584. При этом коррекция амплитуды выполняется по разным алгоритмам для ближнего (до 20 толщин стенки) и для дальнего поля (см. Рис. 5):

if             DST1 < D20 then             

Ac = A + DST1 * (At20/D20)                                                                            для ближнего поля

else       Ac = A + At20 + (DST1-D20) *(Atmax — At20) / (Dmax — D20)       для дальнего поля

здесь:

• Ac: восстановленная локационная амплитуда первого импульса лоцированного события в дБ
• A:  зарегистрированная амплитуда (первого импульса лоцированного события) в дБ
• DST1: вычисленное расстояние от ПАЭ, первым зарегистрировавшим событие, до источника
• At20: ослабление на расстоянии «20 толщин стенки» от источника или амплитуда источника минус измеренная амплитуда на расстоянии D20
• D20: 20 толщин стенки объекта в единицах локации, например, в см
• Atmax: Ослабление на максимальном расстоянии регистрации или максимальная амплитуда минус порог
• Dmax: максимальное расстояние регистрации при данном пороге в единицах локации.

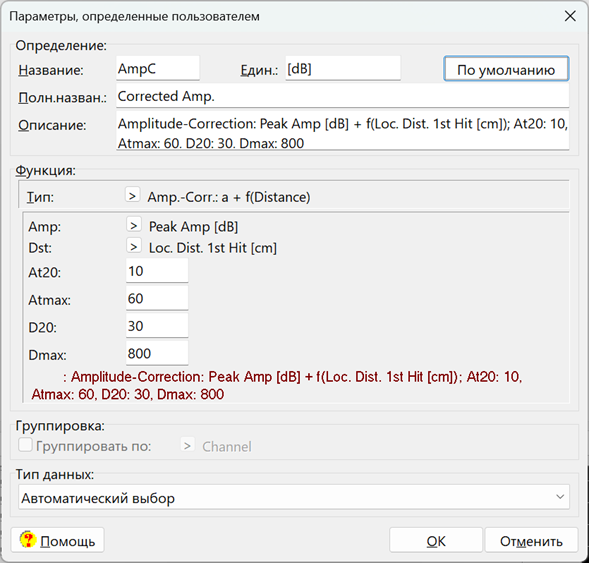
Рис. 5. Пример функции Коррекции Амплитуды

Как правило, в качестве аргументов функции коррекции амплитуды используют расстояние от источника до ПАЭ, первым зарегистрировавшим событие, и соответствующую амплитуду. 

Для правильного применения функции коррекции амплитуды МП должен стоять после локационного процессора. Восстановленная локационная амплитуда используется, например, при оценке опасности источников АЭ в стандарте EN 14584.

Функции Скорости изменения АЭ параметра (Rates)

Функции Скорости изменения параметра служат для определения скорости изменения параметров АЭ импульсов:

если дана переменная (b) — обычно значение параметра или время и интервал ее изменения (ΔB), а также суммарное значение другой переменной (x) — обычно энергия, импульсы, длительность… в этом интервале ΔB, то:

Sum1 = Σx вычисленная в текущем интервале (b-ΔB .. b),

Sum2 = Σx вычисленная в предыдущем интервале (b-2ΔB .. b-ΔB).

С помощью Sum1 и Sum2 определяются следующие функции скорости:

Rate1: Sum1 / ΔB, или полное выражение Σ(x[b-ΔB]..x[b]) / ΔB;

Rate1 – это значение суммарного параметра АЭ (выбросов, энергии..) на интервале изменения параметра нагружения (давления или времени), т.е., фактически, скорость накопления АЭ параметра. При определении функции задаются параметры АЭ и нагружения, а также величина интервала изменения.

Таким образом, Rate1 – это накопление АЭ параметра на единицу изменения параметра нагружения, т.е. скорость, размерность соответствующая – единицы АЭ параметра/единицы параметра нагружения. Оценка скорости накопления АЭ параметров включена во многие системы критериев: ASTM E569, MONPAC.

Величина интервала изменения параметра нагружения имеет значение для определения скорости накопления АЭ параметра. Ее можно выбирать в диапазоне от 0,1% до 10% от максимального значения параметра нагружения (или диапазона времени). Максимальное значение Rate1 не ограничено, минимальное – стремится к нулю.

Как Rate1, так и Rate2 и Rate3, если строятся от изменения параметра нагружения, сильно реагируют на выдержки давления, особенно если выдержка находится в начале рассматриваемого диапазона, поскольку в течение выдержки не происходит существенных изменений параметра нагружения, а параметр АЭ регистрируется. Вследствие этого Rate получает экстремально большие значения. В этом случае есть смысл задавать эти параметры от времени, предполагая, что параметр нагружения изменяется пропорционально или использовать для анализа только периоды чистого нагружения, без выдержек.

Rate2: Sum1 / Sum2, или полное выражение Σ(x[b-ΔB]..x[b]) / Σ(x[b-2ΔB]..x[b-ΔB]);

Rate2 – это отношение суммы параметра АЭ (выбросы, энергия..) на текущем интервале к сумме этого параметра на предыдущем интервале. При определении функции задаются параметр АЭ, параметр нагружения, величина интервала изменения параметра нагружения, а также минимальное значение Sum2.

Если вычисленное значение Sum2 меньше минимально заданного, используется заданное.

Rate2 – это безразмерная величина, характеризующая приращение АЭ параметра на текущем интервале по отношению к предыдущему. Максимальное значение не ограничено, минимальное – стремится к нулю.

К Rate2 относятся все те же положения о выборе и величине параметра нагружения, что и для Rate1.

Может быть применен для оценки выполнения критерия накопления энергии стандарта EN 14584: в течение двух последовательных интервалов пятипроцентного изменения нагрузки суммарная зарегистрированная энергия по одному или более каналов удваивается. Т.е., если значение соотношения Sum1/Sum2 по любому каналу становится более 2, то критерий нарушен, при условии, что ΔB соответствует 5% изменению нагрузки.

Rate3: Sum1 / (Sum1 + Sum2), или полное выражение Σ(x[b-ΔB]..x[b]) / Σ(x[b-2ΔB]..x[b]).

Rate3 – это отношение суммы параметра АЭ (выбросы, энергия..) на текущем интервале к сумме параметра АЭ на предыдущем и текущем интервалах. При определении функции задаются параметр АЭ и величина интервала.

Rate3 – также, как и Rate2 — безразмерная величина, диапазон – от 0 до 1, максимальное значение – стремится к единице (энергия нарастает), минимальное – стремится к нулю (суммарная энергия не нарастает). Физический смысл – аналогичен Rate2, но позволяет лучше оценить изменение накопления параметра. 

Rate1, Rate2 или Rate3 используются для описания дискретных данных (таких как параметры импульса, статусные или параметрические наборы данных) в непрерывном виде: энергия за временной интервал или импульсы за интервал изменения давления. Для дискретных, периодически генерируемых параметров, таких как ENYS (энергия в течение интервала между генерацией статусных сообщений) выбор ΔB является особенно важным. Если значение ΔB близко к значению интервала генерации параметра, то малые изменения ΔB могут привести к большим изменениям в скорости. Этот эффект вызван тем фактом, что при большом ΔB рассматривается большое количество значений параметра, тогда как для малых ΔB некоторые значения не учитываются. Этот эффект может быть уменьшен, если значение ΔB выбирается больше интервала генерации соответствующего параметра.

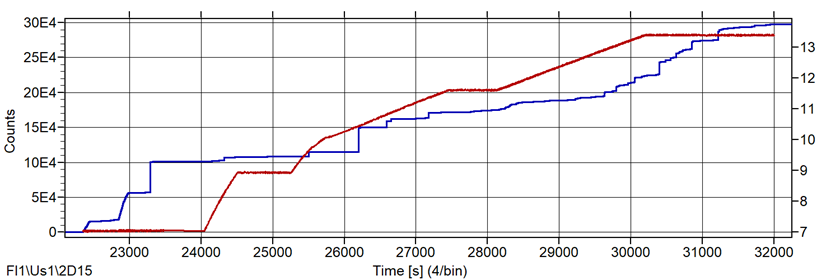
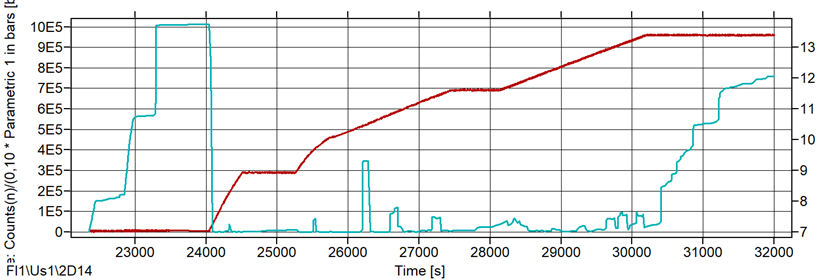
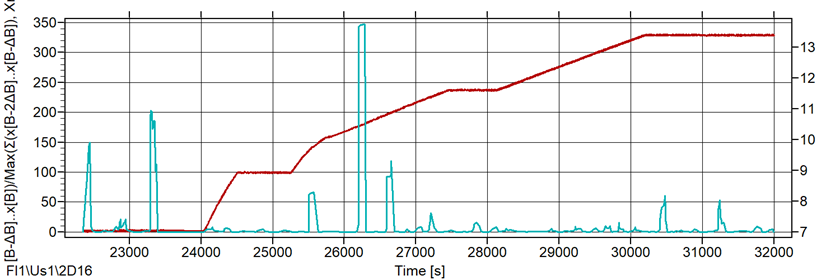
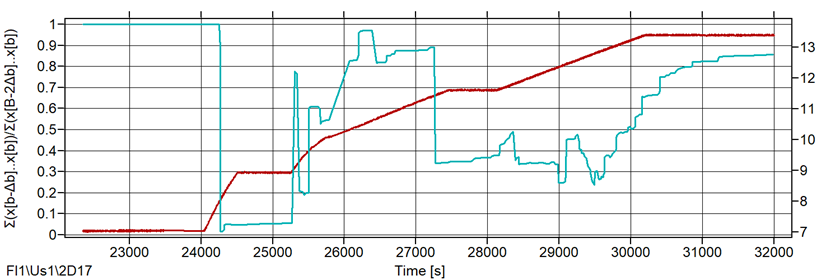
Рис. 6. Накопление выбросов: Counts/Time; Cum/Counts/Time; Rate1: b=0,1 bar; Rate2: b=100 c; Rate3: b=1,0 bar

Функции скоростей могут применяться, если в файле данных имеет место параметр нагружения – от датчика давления или искусственный. Как альтернатива, в качестве параметра нагружения может использоваться время контроля. Результаты применения функций скоростей с разными параметрами приведены на рис. 6 для аргумента «Количество выбросов».

Функции скоростей весьма критично относятся к выбору величины интервала изменения параметра нагружения и результат работы функции сильно зависит от этого значения. Экспериментально определено, что значительные изменения в результатах работы функций имеют место, когда значение b приближается к 0,001 от измеряемого давления. Это происходит, в т.ч. потому, что функции начинают работать в зоне флуктуации измерения давления. В целом, нужно представлять себе результат работы данных функций, проверять его в соответствующих таблицах и диаграммах.

Скорость изменения параметра (Parametric Slope)

Функция определяет скорость изменения параметра (или наклон линии изменения параметра), например параметра нагружения – увеличения/снижения давления в бар/мин.

Алгоритм вычисления скорости изменения параметра – вычисление ΔP/Δt, то есть определение увеличения/уменьшения давления как функции времени.

По умолчанию в качестве параметра нагружения выбирается параметр PA0U —  значение по параметрическому входу 1 в единицах пользователя (например, в барах, см. Рис. 7).

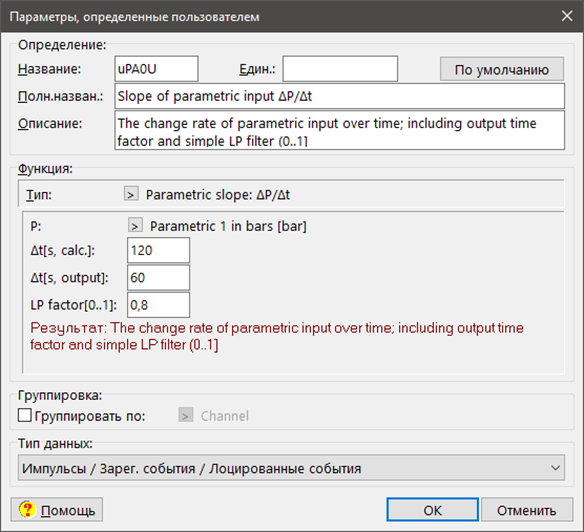
Рис. 7. Окно определения функции скорости изменения параметра

Параметр Δt[s, calc.] должен быть указан в секундах и определяет временное окно Ts. Временное окно Ts делится примерно на 100 равных интервалов. В конце каждого интервала из параметрических данных генерируется выборка. Выборки обычно генерируются путем интерполяции соответствующих параметрических данных, которые происходят до и после точки выборки. На основе выборок во временном окне Ts используется линейная аппроксимация методом наименьших квадратов для получения скорости изменения параметра.

Параметр Δt[s, output] должен быть также указан в секундах. Он определяет масштабирование выходных  результатов. Для масштабирования бар/минуту установите параметр на 60 секунд, а для масштабирования бар/секунду установите параметр на 1 секунду.

Аргумент LP factor[0..1] не имеет размерности и может быть выбран в интервале (0…1). Он определяет вес новых значений в экспоненциальное взвешенное среднее. Значение 1 отключает усреднение и соответствует ситуации, когда результирующее среднее определяется только последней выборкой. По мере уменьшения веса влияние последней выборки на среднее также уменьшается. Для малых значений среднее изменяется очень медленно (результат становится крайне сглаженным). Рекомендуется задавать данный параметр от 0,7 до 0,9.

Применение данной функции с аргументами Δt[s, calc.]=120; Δt[s, output]=60; LP=0,8 для результатов гидравлического испытания сферического резервуара показаны на рис. 8. Видно, что скорость нагружения на некоторых этапах достигала 0,29 и 0,17 бар в минуту.

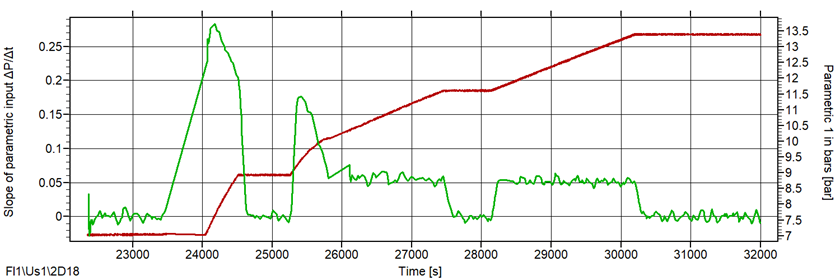
Рис. 8. Гидравлическое испытание сферического резервуара

Процессор ECP или Командный процессор

Командный процессор представляет собой расширение Математического Процессора и включает встроенный язык программирования, позволяющий выполнять над АЭ записями любые операции. Так, например, с помощью математического процессора может быть произведена оценка результатов АЭК по локально-динамическому критерию.

Командный процессор основан на языке программирования Lua. Особенности использования КП приведены в руководстве «Embedded Code Processor. User Manual», описание языка программирования в реализации Vallen Systeme – в руководстве «ECP: LUA Scripting Language Reference Manual». В целом Lua и основы программирования на этом языке изложены в книге«Программирование на языке Lua» Роберту Иерузалимски, а также на сайте https://antirek.github.io/luabook/.

Для использования КП необходимо задать набор входных (любые параметры АЭ записи, данные МП или результаты обработки TR записей) и выходных параметров. Входные параметры – это параметры, которыми оперирует программный код КП. Выходные параметры – это параметры, которые формируются КП. Во вкладке «Выполнение» формируется код процессора (см. Рис. 9). Поставка КП включает несколько небольших примеров использования КП: простой счетчик, вычисление амплитуды в мкв по амплитуде в дБ, формирование количества элементов кластера по его номеру.

Минимальный код программы на Lua для КП состоит из секций:

<ECP_ExecuteOnReset>
-- вставьте сюда код для инициализации, если инициализация не нужна, секция может быть исключена
</ECP_ExecuteOnReset>

<ECP_ExecuteOnDataSet>
-- здесь код, выполняемый для каждого обрабатываемого элемента файла данных
</ECP_ExecuteOnDataSet>

Так, простая программе вычисления амплитуды в микровольтах по амплитуде в дБ выглядит так:

<ECP_ExecuteOnDataSet>
-- test simple transform to uV
if A then 
  return 10^(A / 20) 
end
</ECP_ExecuteOnDataSet>

Практическое применение — исключающая фильтрация

Пример практического применения КП — исключающая фильтрация данных. При испытании по каналу №45 была зарегистрирована помеха предположительно электрического происхождения. Определено, что помеха имеет следующие параметры:

Амплитуду от 44 до 50 дБ и Время Нарастания от 107 до 160 мкс для разных периодов испытания. CHAN, A, R, TS определены как входные, а Accptd – как выходной параметр.

В результате работы КП параметру Accptd импульсов, параметры которых рассматриваются как характерные для помехи, присваивается значение «0». Параметр Accptd прочих импульсов имеет значение «1» (см. Рис. 9). Далее данные фильтруются по параметру Accptd.  Результат совместной работы КП и ПФ представлен на Рис. 10.

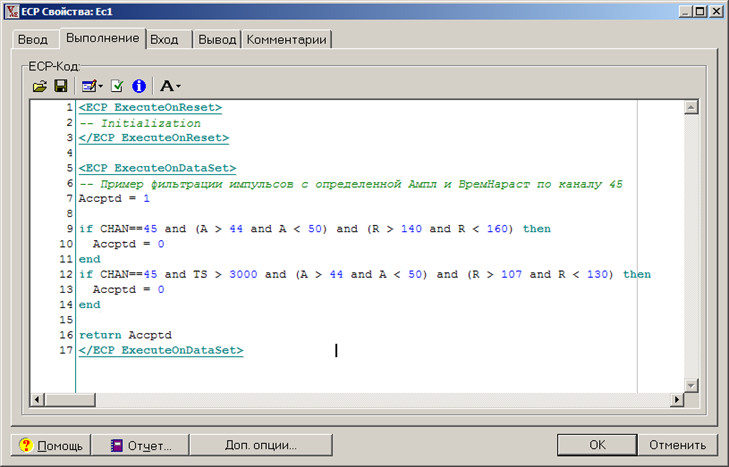
Рис. 9. Пример кода командного процессора

Рис. 10. Исходные данные (диаграммы 2D5 и 2D6) и результат фильтрации (2D7 и 2D8)

Пример импорта параметрических данных

Пример программы импорта параметрических данных из текстового файла приведен в руководстве «ECP: LUA Scripting Language Reference Manual». Текстовый файл, содержащий отметки времени и соответствующие им величину нагрузки, можно сформировать в любом текстовом редакторе:

Time(s)	Pressure (MPa)
0;2,00
1500;2,00
9600;4,00
10600;4,00
16020;5,00
17500;5,00
21700;6,00
23100;6,00
32800;8,00
34100;8,00
42970;9,75
43500;9,75

Программа импорта параметрических данных из текстового файла использует время АЭ записи в секундах (TS) и (P) как выходной параметр. Комментированный текст программы приведен ниже, результат – на Рис. 11.

<ECP_Input>
TS – Время в секундах 
</ECP_Input>

<ECP_ExecuteOnReset>
–- здесь должен быть полный маршрут к файлу нагружения
local f = assert(io.open([[..\Load.txt]], "r")) 
-- время (t), параметр нагружения (p, например, давление),
-- коэффициент (k, наклон)
t,p,k = 0, 0, 0;
--пропускаем первую строку (заголовок)
f:read("*line");
-- объявляем функцию
function read_line()
-- считываем строку из файла
local line = f:read("*line");
-- если достигнут конец файла
if (not line) then 
return false 
end;
-- на случай других разделителей целой и дробной части: замена "," на "."
line = string.gsub(line, ",", ".");
-- ищем разделитель внутри строки
local i = string.find(line, "[;: ]");
-- получаем значения
local t1, p1 = tonumber(string.sub(line, 1, i-1)), tonumber(string.sub(line,i+1));
-- определяем «наклон» между точками (t,p) and (t1,p1)
if(t1==t) then k = 0 
else k = (p1 - p) / (t1 - t); 
end;
-- заменяем значения (t,p) на (t1,p1)
t, p = t1, p1;
return true;
end;
</ECP_ExecuteOnReset>

<ECP_ExecuteOnDataSet>
-- считываем данный из файла нагружения и останавливаемся, когда значение t становится больше 
-- чем TS (время записи в секундах)
while TS > t do
-- считываем следующую строку;
-- возвращаем последнее значение (p) когда достигнут конец файла      
if not read_line() then return p;
      	end;
end;
-- интерполируем значение p для TS с помощью t и t1
return p - k * (t-TS);
</ECP_ExecuteOnDataSet>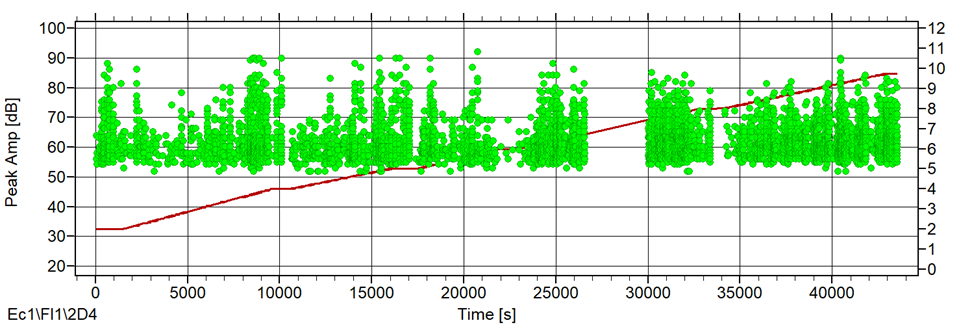

Рис. 11. Результаты импорта данных нагружения из текстового файла

Разбор примера вычисления Ib-value

Ib-value (Improved b-value)– это параметр, используемый для оценки повреждений, например, композитных материалов. Значение b-value изначально использовалось для сейсмологических приложений и определялось в соответствии с формулой Гутенберга-Ричера:

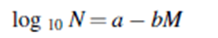
где N — общее количество землетрясений, больших чем M в конкретном регионе и периоде, a — эмпирическая константа, а b — хорошо известное b-value, соответствующее наклону линейной зависимости.

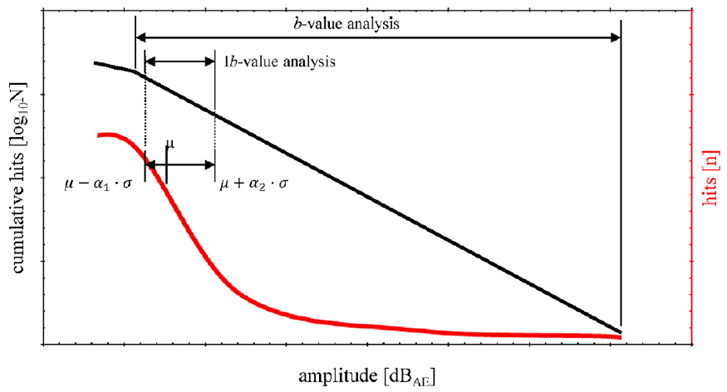
Рис. 12. Анализ b-value и Ib-value

Этот анализ был применен к сигналам АЭ, измеренным в разрушающемся материале в течение заданного времени и под заданной нагрузкой, следующим образом:

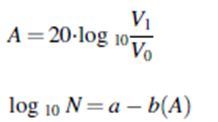
где A — амплитуда сигнала AE, измеренная в децибелах (дБ_АЭ), а N — количество импульсов AE, накопленных до момента регистрации A в течение рассматриваемого периода времени. Амплитуда напрямую связана с уровнем повреждений. B-value, определенное как общий наклон распределения амплитуд в соответствии с кумулятивными импульсами (т.е. наклон черной линии), оказалось эффективным показателем для характеристики образования и роста трещин в течение рассматриваемого периода времени. На практике это глобальный параметр мониторинга, подходящий для характеристики сигналов, возникающих в результате случайных процессов, таких как землетрясения или сигналы АЭ.

Вычисление b было модифицировано для получения Ib-value путем включения статистических параметров распределения амплитуд. При вычислении Ib-value диапазон амплитуды определяется с использованием среднего значения (μ), стандартного отклонения (σ), верхней амплитуды (α1⋅σ) и нижней амплитуды (α2⋅σ):

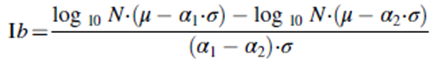
где (α1 — α2)⋅σ — интервал амплитуд. Высокие значения b-value или Ib-value указывают на уровень дефектов, при котором микроскопические трещины доминируют над макроскопическими трещинами, тогда как низкое значение b(Ib) указывает на то, что доминируют макротрещины [3].

Ниже приведен комментированный текст программы, которая поставляется в составе VisualAE, и которая разработана на основе алгоритма Dr. Tomoki Shiotani. Программа использует возможности ECP для расчета Ib-value.

<ECP_Input>
A                  -- Амплитуда в дБ
DSET               -- Номер записи
</ECP_Input>

<ECP_ProcessType>
WantHit            -- Обрабатываются только записи импульсов, но здесь ни на что не влияет
--WantPax
--WantStatus
--WantLabel
--WantEvent
--WantSubhit
</ECP_ProcessType>

--Выход процессора
<ECP_Output>
ib=improved b-value      -- ИБ-значение
Mean=Mean                -- среднее
StdDev=StdDev            -- среднее отклонение
a1=low limit for IB(A1)  -- Нижний предел IB
a2=high limit for IB(A2) -- Верхний предел IB
</ECP_Output>

<ECP_Title>
ECP calculating improved b-value
</ECP_Title>

-- Заголовок, авторские права
<ECP_ApplicationText>
Acknowlegement:
The "Improved b-Value" (ib) algorithm has originally been developed by
Dr. Tomoki Shiotani, Tobishima Corp. Japan.
===========================================
Vallen-Systeme GmbH appreciates Dr. Shiotani's generous allowance to
implement and use his algorithm for the free of cost demonstration of
Embedded Code Processing (ECP) in VisualAE.
</ECP_ApplicationText>

-- Здесь все что должно происходить один раз при запуске программы, а также описания функций
<ECP_ExecuteOnReset>
-- Загружаем модуль List (список). Модуль List находится в папке C:\Vallen\ECP\
-- реализация List – в соответствии с книгой «Программирование на языке Lua» Роберту Иерузалимски
local List=require("List")
-- считываем параметры, которые должны быть заданы в Редакторе переменных
-- или задаем по умолчанию Alpha1, Alpha2, Beta
-- конкретные значения зависят от материала, в диапазоне от 0.5 до 5 (обычно от 0.5 до 1.5)
local Alpha1 = VAEVariables.Alpha1
if not Alpha1 then
  Alpha1 = 1
  print("VAE variable Alpha1 not found, using default value") –- вывод в протокол
end

local Alpha2 = VAEVariables.Alpha2
if not Alpha2 then
  Alpha2 = 1
  print("VAE variable Alpha2 not found, using default value")
end

--количество импульсов (Beta) для расчета, ниже этого количества Ib-value  не определено
local Beta = VAEVariables.Beta
if not Beta then
  Beta = 50
  print("VAE variable Beta not found, using default value")
end

-- Выводим значения этих параметров в протокол
-- Итак, по умолчанию  Alpha1=1, Alpha2=1, Beta=50
print("Using Alpha1, Alpha2, Beta = ", Alpha1, Alpha2, Beta)

--Определяем переменную, макс кол-во импульсов для запоминания, равную Beta (По умолчанию = 50)
local MaxHits = Beta

-- задаем очередь импульсов Hits типа List (только амплитуды)
local Hits = List()
-- количество сохраненных импульсов изначально равно 0, вызываем ф-цию count для проверки
local HitCnt = Hits:count()
print("HitCnt = ", HitCnt)
-- Задаем сумму амплитуд, сумму квадратов амплитуд, максимальную амплитуду. Обнуляем
local SumAmp = 0
local SumSquare = 0
local MaxAmp = 0     -- maxamp, нужна, когда n2==0

-- ----------------------------------------------------------------------
-- Функция обрабатывает (сохраняет, прибавляет) Импульсы. Работает для каждого очередного
-- импульса. Получает на вход Амплитуду
function StoreHit(Amp)

  Hits:pushright(Amp)    -- добавляет амплитуду в правую позицию очереди, увеличивается количество элементов списка
  HitCnt = Hits:count()  		-- получаем количество элементов очереди
  SumAmp    = SumAmp + Amp           -- прибавляем амплитуду к сумме амплимтуд
  SumSquare = SumSquare + Amp * Amp  -- прибавляем квадрат амплитуды к сумме квадратов амплитуд

  if (MaxAmp) then    -- проверка на то, что МаксАмп определена, т.е. не nil
    if Amp > MaxAmp then
        MaxAmp = Amp -- обновляем MaxAmp, если текущая амплитуда Amp больше MaxAmp
    end
  end

-- Сообщения могут использоваться для отладки
--  print("Amp = ", Amp)
--  print("Hits[0],Hits[1], Hits[HitCnt-1], Hits[HitCnt] =", Hits[0], Hits[1], Hits[Hits:count()-2], Hits[Hits:count()-1])
--  print("MaxAmp = ", MaxAmp)      
--  print("SumAmp 1 = ", SumAmp)
--  print("MaxHits = ", MaxHits)
--  print("HitCnt = ", HitCnt)
--  print("Hits:count()= ", Hits:count())
--  print("Hits.first =", Hits.first)
--  print("Hits.last =", Hits.last)
-- -----------------------------------
-- Цикл начинает работать когда количество накопленных импульсов HitCnt начинает
-- превышать предварителльно заданный MaxHits
-- Убирает первый элемент списка из списка и из всех параметров СуммАмп, СуммКвадрАмп, МаксАмп
  while (HitCnt > MaxHits) do
    --remove older hit
    local Amp = Hits:popleft()  -- убирает левый элемент списка (самый старый), сдвигая его влево
    SumAmp    = SumAmp - Amp            -- убирает его из суммы амплитуд
    SumSquare = SumSquare - Amp * Amp   -- убирает его из суммы квадратов амплитуд
    HitCnt = HitCnt - 1                 -- и уменьшает на 1 сумму импульсов
    --если MaxAmp будет удаляется, нам придется искать его снова
    if (MaxAmp and (Amp >= MaxAmp)) then
       MaxAmp = nil                      -- если извлеченная Амп больше либо равна МаксАмп
    end                                  -- присваиваем MaxAmp nil – развоплощаем ее
  end
end
-- ----------------------------------------------------------------------
function ProcessIB()
  -- ждем накопления не менее Beta импульсов 
  if HitCnt < Beta then 
return 
  end   			-- если накоплено недостаточно импульсов - выходим из функции

-- если накоплено достаточно, то для каждого импульса:

  local mean   = SumAmp / HitCnt      -- определяем среднюю амплитуду и стандартное отклонение
  local stddev = math.sqrt( (SumSquare - (SumAmp * SumAmp / HitCnt)) / (HitCnt - 1) )
  local a1 = mean - Alpha1 * stddev   -- определяем мин и макс значение анализируемого диапазона
  local a2 = mean + Alpha2 * stddev   -- амплитуд

  local i, a
  local n1, n2 = 0, 0

-- вычисляем hits, N(w1) and N(w2)
  for i = Hits.first, Hits.last do  -- цикл от первого до последнего элемента списка
    a = Hits[i]                     -- a1 всегда < a2, поэтому используем небольшую оптимизацию
    if a >= a1 then                 -- присваиваем амплитуду элемента списка
      n1 = n1 + 1                   -- считаем количество импульсов выше ампл a1 (n1) и a2 (n2)
      if a >= a2 then 
        n2 = n2 + 1 
      end
    end
  end
  -- обрабатываем исключительные ситуации
  -- если n2 == 0, ib не может быть корректно вычислен
  -- обычно это значит, что Alpha2 должно быть уменьшено
  if n2 == 0 then                               -- если n2=0, т.е. выше a2 импульсов нет,
    print('a2 is too high, check Alpha2 value') -- то Alpfa2 назначен слишком большим
    -- устанавливаем верхнюю амплитуду на максимальную найденную
    -- в противном случае ib-value будет ниже
    -- нужно пересчитать MaxAmp
    if MaxAmp == nil then                   -- если (при этом) МаксАмп не определен,
      MaxAmp = a1                           -- присваиваем МаксАмп значение a1
      --print('lookup max amp')
      for i = Hits.first, Hits.last do      -- проходим по массиву
        a = Hits[i]                         -- присваиваем амплитуду элемента списка
        if a > MaxAmp then 
          MaxAmp = a 
        end   -- если очередная Амп больше МаксАмп, присваиваем МаксАмп ее значение
      end
    end
    n2 = 1                                  -- присваиваем n2 значение 1
    a2 = MaxAmp                             -- a2 - значение МаксАмп
  end

  --calculate ib!
  ib = math.log10(n1 / n2) / (a2 - a1)      -- вычисляем ib-value по известной формуле
  --ib = (math.log10(n1) - math.log10(n2)) / (a2 - a1);

  --debug only
  --print(a1, a2, n1, n2);
  return ib, mean, stddev, a1, a2, MaxAmp
end;

</ECP_ExecuteOnReset>

<ECP_ExecuteOnDataSet>
-- ----------------------------------------------------------------------
-- Основной цикл программы
-- insert loop code here
-- print(VAEVariables.LastLabelText)
  print("----------------")

  StoreHit(A)

  local ib, mean, stddev, a1, a2, MaxAmpl = ProcessIB()
  -- we could multiply ib with 20, as some authors suggest
  -- in order to get values around 1
  -- возвращаем 20*ib и т.д.
  return ib and 20*ib, mean, stddev, a1, a2, MaxAmpl
-- ----------------------------------------------------------------------
</ECP_ExecuteOnDataSet>

В приведенном листинге нужно отметить следующие особенности:

• Отладка программы через функцию print, которая передает информацию в протокол.
• Использование внешних модулей для определения нового типа данных (очередь).

Использованию и вычислению Ib-value посвящен ряд статей, некоторые из которых приведены ниже:

1. T. Shiotani, S. Yuyama, Z. W. Li and M. Ohtsu. Application of ae improved b-value to quantitative evaluation of fracture process in concrete materials.
2. Acoustic Emission Testing and Ib-Value Analysis of Ultraviolet Light-Irradiated Fiber Composites. Doyun Jung and Wonjin Na.
3. Use of acoustic emission b(Ib)-values to quantify damage in composites. Doyun Jung, Woong-Ryeol Yu, Wonjin Na.

Этот обзор в PDF